قوانين الفصل الخامس فيزياء ثالث ثانوي |

يتم عرض قوانين الفصل الخامس فيزياء ثالث ثانوي و هو إزدواجية المادة و الجسيم. و القوانين نبدأها بقانون بلانك و قانون فين ثم قانون أينشتاين و قوانين أنبوبة أشعة الكاثود. مرورا بعلاقة اينشتين و دي برولي و قوانين الفوتونات.

تعد القوانين من أهم أجزاء منهج الفيزياء حيث تدور المادة حول فهم القوانين والتطبيق عليها. فمن المهم معرفة القوانين ومراجعتها من وقت إلى أخر. في هذا المقال ملخص قوانين الفصل الخامس “إزدواجية المادة و الجسيم” فيزياء للصف الثالث الثانوى. يمكنك الأطلاع على قوانين الفصل الأول و الثاني و الثالث و الرابع و السادس.

نبدأ بالثوابت المهمة

$h = 6.625 x 10^{-34} j.s$ ثابت بلانك
$c = 3.00 x 10^{8} m/s$ سرعة الضوء
$m_{e} = 9.11 x 10^{-31} Kg$ كتلة الألكترون
$Q_{e} = 1.6 x 10^{-19} C$ شحنة الألكترون

قانون بلانك

و يعد أهم قوانين الفصل الخامس فيزياء ثالث ثانوي. طاقه كل فوتون تتناسب مع تردده و من ثم $E = h \nu$ حيث (h) ثابت بلانك .

أو بدلالة الطول الموجي $E = \frac{hc}{\lambda}$

قانون الطول الموجي

حيث العلاقة بين الطول الموجي و التردد
$\lambda = \frac{c}{\nu}$

طاقة شعاع من الفوتونات عددها n و لها نفس التردد $E =n h \nu$ أو $E = \frac{nhc}{\lambda}$

قانون فين

الذي يمثل التناسب العكسي بين درجة الحرارة الكلفينية و الطول الموجي المصاحب لأكبر شدة إشعاع.

$\frac{\lambda_{m1}}{\lambda_{m2}} = \frac{T_2}{T_1}$

قانون فين للإزاحة العلاقة بين الطول الموجي الذي يصاحب أكبر شدة أشعاع و درجة حرارة الجسم المتوهج.

قوانين أنبوبة أشعة الكاثود

بعد تعجيل الألكترونات التي كتلتها m و شحنتها بواسطة فرق جهد V تكتسب طاقة حركة K.E. أي تتحول الطاقة الكهربية إلى كطاقة حركية

$W = K.E$

حيث تكتسب الألكترونات سرعة مقدارها v تتعين من العلاقة

$e.V = \frac{1}{2}m_e v^2$

و أيضا يمكن تعيين الطول الموجي للألكترونات المعجلة من هذه العلاقة

$e.V = \frac{P^2}{2m_e} = \frac{h^2}{2m_e \lambda^2}$

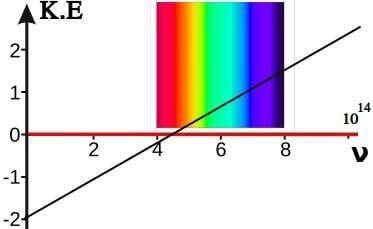
قانون أينشتاين

طاقة الفوتون تستخدم في الظاهرة الكهروضوئية للتغلب على طاقة الشغل و الباقي طاقة حركية

$K.E = h \nu - E_w$

فإذا كان دالة الشغل $E_w = h \nu_c$

$K.E = h \nu - h \nu_c$

و بالتالي فإن

$\frac{1}{2}m_e v^2 = h (\nu - \nu_c)$

علاقة اينشتاين

تستخدم في الربط بين الكتلة m والطاقة E و هي

$E = m c^2$

حيث C سرعة الضوء. علاقة اينشتاين تستخدم في الربط بين الكتلة والطاقة و تستخدم في حساب الطاقة الناتجة عن تحول جزء من الكتلة الى طاقة أو العكس. في المثال المشهور عن تحول الكتلة الى طاقة و هو عملية الإنشطار النووي.

يمكن الربط بين الكتلة و الطاقة و تردد الفوتون من العلاقة

$m c^2 = h \nu$

عند مساواة علاقتي بلانك و اينشتين يمكن استنتاج علاقة تربط بين كتلة الفوتون m أو كمية تحركه p و تردده في معادلة تعبر عن ربط الطبيعة الجسيمية للضوء بالخواص الموجية كالآتي

كتلة الفوتون

$m = \frac{h \nu}{c^2} = \frac{h}{\lambda c}$

كمية تحرك الفوتون

$mc = \frac{h \nu}{c} = \frac{h}{\lambda}$

القوى التي يؤثر بها شعاع ضوئي على سطح عاكس

نجد في النهاية أن العلاقة التي تربط بين قوة شعاع من الضوء و قدرة هذا الشعاع و يقصد بالقدرة هي الطاقة الكامنة في الشعاع الساقط خلال واحد ثانية. و العلاقة هي أن لأي جسم عاكس تكون القوى المؤثرة عليه من شعاع ضوئي منعكس بتساوي

$F = \frac{2 P_w}{C}$

و يمكن كتابة قدرة الشعاع بهذه العلاقة

$P_w = h \nu \Phi_L$

حيث أن $\Phi_L$ هي عدد الفوتونات في الثانية الواحدة.

معادلة دي برولي الفصل الخامس

فإذا كانت كمية تحرك الفوتون هي

$\lambda = \frac{h}{P}$

حيث يتم الربط بين كمية التحرك وهي صفة جسميه والطول الموجي وهي صفة موجيه عن طريق هذه المعادلة بالنسبة للفوتون. وتم افتراض نفس المعادلة بالنسبة للكترون.

طول موجة دي برولي المصاحبة لجسيم متحرك تعطى بالعلاقة

$\lambda = \frac{h}{P}$

الطول الموجي المصاحب للجسم له كمية تحركه P بمعادلة دى براولى حيث هو ثابت بلانك h.

موجات دي برولي

أهم التطبيقات على الطبيعة الموجية للالكترونات هو الميكروسكوب الإلكتروني الذي يمكن تعديل الطول الموجي للالكترون عن طريق اكسابه طاقة حركة الإلكترون. و يمكن كتابة العلاقة بين طاقة حركة الالكترون و طوله الموجي كما يأتي

$e V = K.E = \frac{h^2}{2m\lambda^2}$

والتحكم في الطول الموجي للإلكترون يؤدي إلى التحكم في قوة تكبير الميكروسكوب الالكتروني فكلما زاد الطول الموجي كلما زادت قدرته التكبيريه.